2023年山东省专升本《高等数学Ⅰ》(公共课)考试大纲

　　Ⅰ. 考试内容与要求

　　本科目考试要求考生掌握高等数学的基本概念、基本理论和基本方法， 主要考查考生识记、理解、计算、推理和应用能力，为进一步学习奠定基 础。具体内容与要求如下：

　　一、函数、极限与连续

　　( 一 ) 函数

　　1.理解函数的概念，会求函数的定义域、表达式及函数值，会建立应 用问题的函数关系。

　　2.掌握函数的有界性、单调性、周期性和奇偶性。 3.理解分段函数、反函数和复合函数的概念。 4.掌握函数的四则运算与复合运算。 5.掌握基本初等函数的性质及其图形，理解初等函数的概念。

　　( 二 ) 极限

　　1.理解数列极限和函数极限(包括左极限和右极限)的概念。理解函数 极限存在与左极限、右极限存在之间的关系。

　　2.理解数列极限和函数极限的性质。 了解数列极限和函数极限存在的 两个收敛准则(夹逼准则与单调有界准则)。熟练掌握数列极限和函数极限 的运算法则。

　　3.熟练掌握两个重要极限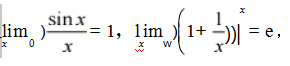，并会用它们求极限。

　　4.理解无穷小量、无穷大量的概念，掌握无穷小量的性质、无穷小量 与无穷大量的关系。会比较无穷小量的阶(高阶、低阶、同阶和等价)。会 用等价无穷小量求极限。

　　( 三 ) 连续

　　1.理解函数连续性 (包括左连续和右连续) 的概念，掌握函数连续与 左连续、右连续之间的关系。会求函数的间断点并判断其类型。

　　2.掌握连续函数的四则运算和复合运算。理解初等函数在其定义区间 内的连续性。

　　3.会利用连续性求极限。

　　4.掌握闭区间上连续函数的性质 (有界性定理、最大值和最小值定理、 介值定理、零点定理)，并会应用这些性质解决相关问题。

　　二、一元函数微分学

　　( 一 ) 导数与微分

　　1.理解导数的概念及几何意义，会用定义求函数在一点处的导数 (包 括左导数和右导数)。会求平面曲线的切线方程和法线方程。理解函数的可 导性与连续性之间的关系。

　　2.熟练掌握导数的四则运算法则和复合函数的求导法则，熟练掌握基 本初等函数的导数公式。

　　3.掌握隐函数求导法、对数求导法以及由参数方程所确定的函数的求 导法，会求分段函数的导数。

　　4.理解高阶导数的概念，会求函数的高阶导数。

　　5.理解微分的概念，理解导数与微分的关系，掌握微分运算法则，会 求函数的一阶微分。

　　( 二 ) 中值定理及导数的应用

　　1.理解罗尔定理、拉格朗日中值定理， 了解柯西中值定理和泰勒中值 定理。会用罗尔定理和拉格朗日中值定理解决相关问题。

　　2.熟练掌握洛必达法则，会用洛必达法则求“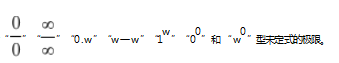

　　3.理解驻点、极值点和极值的概念，掌握用导数判断函数的单调性和 求函数极值的方法，会利用函数的单调性证明不等式，掌握函数最大值和 最小值的求法及其应用。

　　4.会用导数判断曲线的凹凸性，会求曲线的拐点以及水平渐近线与垂

　　直渐近线。

　　三、一元函数积分学

　　( 一 ) 不定积分

　　1.理解原函数与不定积分的概念， 了解原函数存在定理，掌握不定积 分的性质。

　　2.熟练掌握不定积分的基本公式。

　　3.熟练掌握不定积分的换元积分法和分部积分法。

　　4.掌握简单有理函数的不定积分的求法。

　　( 二 ) 定积分

　　1.理解定积分的概念及几何意义， 了解可积的条件。

　　2.掌握定积分的性质及其应用。

　　3.理解积分上限的函数，会求它的导数，掌握牛顿-莱布尼茨公式。

      4.熟练掌握定积分的换元积分法与分部积分法。

      5.会用定积分表达和计算平面图形的面积、旋转体的体积。

      6. 了解反常积分的概念。

　　四、向量代数与空间解析几何

　　( 一 ) 向量代数

　　1.理解空间直角坐标系，理解向量的概念及其表示法，会求单位向量、 方向余弦、向量在坐标轴上的投影。

　　2.掌握向量的线性运算，会求向量的数量积与向量积。 

      3.会求两个非零向量的夹角，掌握两个向量平行、垂直的条件。

　　( 二 ) 平面与直线

　　1.会求平面的点法式方程、一般式方程。会判断两平面的位置关系(垂 直、平行 )。

　　2.会求点到平面的距离。

　　3.会求直线的对称式方程、一般式方程、参数式方程。会判断两直线 的位置关系 (平行、垂直)。

　　4.会判断直线与平面的位置关系 (垂直、平行、直线在平面上)。

　　五、多元函数微积分学

　　( 一 ) 多元函数微分学

　　1.理解二元函数的概念、几何意义及二元函数的极限与连续的概念， 会求二元函数的定义域。

　　2.理解二元函数偏导数和全微分的概念，理解全微分存在的必要条件 和充分条件。掌握二元函数的一阶、二阶偏导数的求法，会求二元函数的 全微分。

　　3.掌握复合函数一阶、二阶偏导数的求法。

　　4.掌握由方程F(x, y, z) = 0 所确定的隐函数z = z(x, y) 的一阶偏导数的计 算方法。

　　5.会求二元函数的无条件极值。

　　( 二 ) 二重积分 1.理解二重积分的概念、性质及其几何意义。 2.掌握二重积分在直角坐标系及极坐标系下的计算方法。

　　六、无穷级数

　　( 一 ) 数项级数

　　1.理解数项级数收敛、发散的概念。掌握收敛级数的基本性质，掌握 级数收敛的必要条件。

　　2.掌握几何级数、调和级数与p 级数的敛散性。

　　3.掌握正项级数收敛性的比较判别法和比值判别法。

　　4.掌握交错级数收敛性的莱布尼茨判别法。

　　5.理解任意项级数绝对收敛与条件收敛的概念。

　　( 二 ) 幂级数

　　1.理解幂级数的概念，会求幂级数的收敛半径、收敛区间和收敛域。 2.掌握幂级数在其收敛区间内的性质(和、差、逐项求导与逐项积分)。 3.掌握幂级数的和函数在其收敛域上的性质。

　　4.会利用逐项求导和逐项积分求幂级数的和函数。

　　5.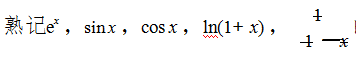的麦克劳林级数，会将一些简单

　　的初等函数展开为x 一 x0 的幂级数。

　　七、常微分方程

　　( 一 ) 一阶微分方程

　　1.理解微分方程的定义，理解微分方程的阶、解、通解、初始条件和 特解等概念。

　　2.掌握可分离变量微分方程的解法。

　　3.掌握一阶线性微分方程的解法。

　　( 二 ) 二阶线性微分方程

　　1.理解二阶线性微分方程解的结构。

　　2.掌握二阶常系数齐次线性微分方程的解法。

　　Ⅱ. 考试形式与题型范围

　　一、考试形式

　　考试采用闭卷、笔试形式。试卷满分 100 分，考试时间 120 分钟。

        二、题型范围

　　  选择题、填空题、判断题、计算题、解答题、证明题、应用题。